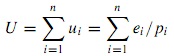Crystalline Silicon -- The Ideal Crystal

Local Mobile Advertising
Local Coupons

A large single crystal of pure silicon forms the starting point for the monocrystalline silicon solar cell –  the most efficient type in common use. As we shall see, the simple and elegant structure of such crystals makes it comparatively easy to explain the basic semiconductor physics and operation of PV cells. We are talking here of silicon refined to very high purity, similar to that used by the electronics industry to make semiconductor devices (diodes, transistors, and integrated circuits including computer chips). Its purity is typically 99.99999%. This contrasts with the far less pure metallurgical grade silicon, produced by reducing quartzite in electric arc furnaces, that is used to make special steels and alloys.

The   Czochralski (CZ)  method of growing silicon crystals is quite easy to visualize. Chunks of pure silicon with no particular crystallographic structure are melted at 1414°C in a graphite crucible. A small seed of silicon is then brought into contact with the surface of the melt to start crystallization. Molten silicon solidifi es at the interface between seed and melt as the seed is slowly withdrawn. A large ingot begins to grow both vertically and laterally with the atoms tending to arrange themselves in a perfect crystal lattice.

Unfortunately, this classic method of producing crystals has a number of disadvantages. Crystal growth is slow and energy intensive, leading to high production costs. Impurities may be introduced due to interaction between the melt and the crucible. And in the case of PV the aim is of course to
produce thin solar cell wafers rather than large ingots, so wire saws are used to cut the ingot into thin slices, a time consuming process that involves discarding valuable material. For these reasons the PV industry has spent a lot of R & D effort investigating alternatives, including pulling crystals in thin sheet or ribbon form, and some of these are now used in volume production. Whatever method is employed, the desired result is pure crystalline silicon with a simple and consistent atomic structure.

The element silicon has atomic number 14, meaning that each atom has 14 negatively charged electrons orbiting a positively charged nucleus, rather like a miniature solar system. Ten of the electrons are tightly bound to the nucleus and play no further part in the PV story, but the other four   valence electrons  are crucial and explain why each atom aligns itself with four immediate neighbours in the crystal. This is illustrated by Figure  2.4 (a). The  ‘ glue ’  bonding two atoms together is two shared valence electrons, one from each atom. Since each atom has four valence electrons that are not tightly bound to its nucleus, a perfect lattice structure is formed when each atom forms bonds with its four nearest neighbours (which are actually at the vertices of a three - dimensional tetrahedron, but shown here in two dimensions for simplicity). The structure has profound implications for the fundamental physics of silicon solar cells.

Silicon in its pure state is referred to as an intrinsic  semiconductor. It is neither an insulator like glass, nor a conductor like copper, but something in between. At low temperatures its valence electrons are tightly constrained by bonds, as in part (a) of the figure, and it acts as an insulator. But bonds can be broken if sufficiently jolted by an external source of energy such as heat or light, creating electrons that are free to migrate through the lattice. If we shine light on the crystal the tiny packets, or quanta, of light energy can produce broken bonds if sufficiently energetic. The silicon becomes a conductor, and the more bonds are broken the greater its conductivity.

Figure  2.4 (b) shows an electron ε1 that has broken free to wander through the lattice. It leaves behind a broken bond, indicated by a dotted line. The free electron carries a negative charge and, since the crystal remains electrically neutral, the broken bond must be left with a positive charge. In effect it is a positively charged particle, known as a   hole.  We see that breaking a bond has given rise to a pair of equal and opposite charged  ‘ particles ’ , an electron and a hole. Not surprisingly they are referred to as an electron-hole pair.

At first sight the hole might appear to be an immovable object fixed in the crystal lattice. But now consider the electron ε2  shown in the figure, which has broken free from somewhere else in the lattice. It is quite likely to jump into the vacant spot left by the first electron, restoring the original broken bond, but leaving a new broken bond behind. In this way a broken bond, or hole, can also move through the crystal, but as a positive charge. It is analogous to a bubble moving in a liquid; as the liquid moves one way the bubble is seen travelling in the opposite direction.

We see that the electrical properties of intrinsic silicon depend on the number of mobile electron–hole pairs in the crystal lattice. At low temperatures, in the dark, it is effectively an insulator. At higher temperatures, or in sunlight, it becomes a conductor. If we attach two contacts and apply an external voltage using a battery, current will flow – due to free electrons moving one way, holes the other. We have now reached an important stage in understanding how a silicon wafer can be turned into a practical solar cell.

Yet there is a vital missing link: remove the external voltage and the electrons and holes wander randomly in the crystal lattice with no preferred directions. There is no tendency for them to produce current flow in an external circuit. A pure silicon wafer, even in strong sunlight, cannot   generate  electricity and become a solar cell. What is needed is a mechanism to propel electrons and holes in opposite directions in the crystal lattice, forcing current through an external circuit and producing useful power. This mechanism is provided by one of the great inventions of the 20th century, the semiconductor   p  –   n  junction. 

Solar Cell

Local Mobile Advertising
Local Coupons

Silicon solar cells have been the workhorse of the PV industry for many years and currently account for well over 80% of world production. Modules based on these cells have a long history of rugged reliability, with guarantees lasting 20 or 25 years that are exceptional among manufactured products.

Although cells made from other materials are constantly being developed and some are in commercial production, it will be hard to dis-lodge silicon from its pedestal. The underlying technology is that of semiconductor electronics: a silicon solar cell is a special form of semiconductor diode.

Fortunately, silicon in the form of silicon dioxide (quartz sand) is an extremely common component of the Earth ’ s crust and is essentially non - toxic. There is a further good reason for focussing strongly on silicon cells in this chapter: in its   crystalline  form silicon has a simple lattice structure, making it comparatively easy to describe and appreciate the underlying science.

There are two major types of crystalline silicon solar cell in current high volume production:

• Monocrystalline.The most efficient type, made from a very thin slice, or wafer, of a large single crystal obtained from pure molten silicon. The circular wafers, often 5 or 6 inches (15cm) in diameter, have a smooth silvery appearance and are normally trimmed to a pseudo - square or hexagonal shape so that more can be fitted into a module. Fine contact fingers and busbars are used to conduct the electric current away from the cells which have a highly ordered crystal structure with uniform, predictable, properties. However, they require careful and expensive manufacturing processes, including  ‘ doping ’  with small amounts of other elements to produce the required electrical characteristics. Typical commer-cial module effi  ciencies fall in the range 12 – 16%. The module surface area required is about 7  m2 /kWp .
• Multicrystalline,      also called   polycrystalline.  This type of cell is also produced from pure molten silicon, but using a casting process. As the silicon cools it sets as a large irregular multicrystal which is then cut into thin square or rectangular slices to make individual cells. Their crystal structure, being random, is less ideal than with monocrystalline material and gives slightly lower cell eficiencies, but this disadvantage is offset by lower wafer costs. Cells and modules of this type often look distinctly blue, with a scaly, shimmering appearance. Multicrystalline modules exhibit typical eficiencies in the range 11 – 15% and have overtaken their monocrystalline cousins in volume production over recent years. The module surface area is about 8 m2 /kWp .     

You have probably already gathered that the eficiency  of any solar cell or module, the percentage of solar radiation it converts into electricity, is considered one of its most important properties. The higher the eficiency, the smaller the surface area for a given power rating. This is important when space is limited, and also because some of the additional costs of PV systems  –  especially mounting and fixing modules  –  are area related. Crystalline silicon cells, when operated in strong sunlight, have the highest efficiencies of all cells commonly used in terrestrial PV systems, plus the promise of modest increases as the years go by due to improvements in design and manufacture. But it is important to realize that other types of cell often perform better in weak or diffuse light, a matter we shall return to in later sections.

Research laboratory cells achieve considerably higher efficiencies than mass - produced cells. This reflects the ongoing R & D effort that is continually improving cell design and leading to better commercial products. In some applications where space is limited and effi ciency is paramount  –  for example, the famous solar car races held in Australia  –  high - quality cells made in small batches are often individually tested for effi  ciency before assembly.

Module efficiencies are slightly lower than cell efficiencies because a module’s surface area cannot be completely filled with cells and the frame also takes up space. It is always important to distinguish carefully between cell and module efficiency.

There is one further type of silicon solar cell in common use:

• Amorphous. Most people have met small amorphous silicon (a - Si) cells in solar - powered consumer products such as watches and calculators that were first introduced in the 1980s. Amorphous cells are cheaper than crystalline silicon cells, but have much lower efficiencies, typically 6 – 8%. Nowadays, large modules are available and suitable for applications where space is not at a premium, for example on building facades. The surface area required is about
  16 m2/kWp .

We focus initially on crystalline silicon solar cells for two main reasons: their comparatively simple crystal structure and theoretical background; and their present dominant position in the terrestrial PV market. Their wafer technology has been around for a long time and is often referred to as  ‘first generation’ ; they are the cells you are most likely to see on houses, factories, and commercial buildings. 

However, it is important to realize that many other semiconductor materials can be used to make solar cells. Most come under the heading of   thin film  –  somewhat confusing because a - Si is also commonly given this title  –  and involve depositing very thin layers of semiconductor on a variety of substrates. Thin  film products are generally regarded as the ultimate goal for terrestrial PV since they use very small amounts of semiconductor material and large - scale continuous production processes without any need to cut and mount individual crystalline wafers. Thin  film modules based on the compound semiconductors   copper indium diselenide (CIS) and cadmium telluride (CdTe)  are in commercial production. Often referred to as ‘second generation’, they currently have efficiencies lower than those of crystalline silicon, but they represent a highly significant advance into thin film products. We will discuss them, and several types of specialized cells and modules later.

Electrostatics

Local Mobile Advertising
Local Coupons

If a conductor has a deficit of electrons, it will exhibit a net positive charge. If, on the other hand, it has a surplus of electrons, it will exhibit a net negative charge. An imbalance in charge can be produced by friction (removing or depositing electrons using materials such as silk and fur, respectively) or induction (by attracting or repelling electrons using a second body which is, respectively, positively or negatively charged).

Force between charges

Coulomb’s Law states that, if charged bodies exist at two points, the force of attraction (if the charges are of opposite polarity) or repulsion (if the charges have the same polarity) will be proportional to the product of the magnitude of the charges divided by the square of their distance apart. Thus:

where Q1 and Q2 are the charges present at the two points (in Coulombs), r the distance separating the two points (in metres), F is the force (in Newtons), and k is a constant depending upon the medium in which the charges exist. In vacuum or ‘free space’, 

 

Combining the two previous equations gives:

Electric fields

The force exerted on a charged particle is a manifestation of the existence of an electric field. The electric field defines the direction and magnitude of a force on a charged object. The field  itself is invisible to the human eye but can be drawn by constructing lines which indicate the motion of a free positive charge within the field; the number of field lines in a particular region being used to indicate the relative strength of the field at the point in question.

Figures 1.7 and 1.8 show the electric fields between charges of the same and opposite polarity while Fig. 1.9 shows the field which exists between two charged parallel plates.

Electric field strength

The strength of an electric field (5) is proportional to the applied potential difference and inversely  proportional to the distance between the two conductors. The electric field strength is given by:   

E = V / d

where E is the electric field strength (V/m), V is the applied potential difference (V) and d is the distance (m).

Example

Two parallel conductors are separated by a distance of 25 mm. Determine the electric field strength if they are fed from a 600 V d.c. supply.

Solution

The electric field strength will be given by:
 


Permittivity

The amount of charge produced on the two plates shown in Fig. 1.9 for a given applied voltage will depend not only on the physical dimensions but also on the insulating dielectric material that appears between the plates. Such materials need to have a very high value of resistivity (they must not conduct charge) coupled with an ability to withstand high voltages without breaking down.

A more practical arrangement is shown in Fig. 1.10. In this arrangement the ratio of charge, Q, to potential difference, V, is given by the relationship:

where A is the surface area of the plates (in m), d is the separation  (in m), and  E is a constant for the dielectric material known as the  absolute permittivity of the material (sometimes also referred to as the dielectric constant).

The absolute permittivity of a dielectric material is the product of the permittivity of free space ( E0) and the  relative permittivity ( Er) of the material. Thus:

The dielectric strength  of an insulating dielectric is the maximum electric field strength that can safely be applied to it before breakdown (conduction) occurs. Table 1  shows values of relative permittivity and dielectric strength for some common dielectric materials.

Electromagnetism

When a current flows through a conductor a magnetic field is produced in the vicinity of the conductor. The magnetic field is invisible but its presence can be detected using a compass needle (which will deflect from its normal North South position). If two current-carrying conductors are placed in the vicinity of one another, the fields will interact with one another and the conductors will experience a force of attraction or repulsion (depending upon the relative direction of the two currents). 

Force between two current-carrying conductors

The mutual force which exists between two parallel current-carrying conductors will be proportional to the product of the currents in the two conductors and the length of the conductors but inversely proportional to their separation. Thus:

where  I1 and  I2 are the currents in the two conductors (in Amps), l is the parallel length of the conductors (in metres), d is the distance separating the two conductors (in metres),  F is the force (in Newtons), and  k is a constant depending upon the medium in which the charges exist.  In vacuum or ‘free space’,

Combining the two previous equations gives:

Magnetic fields

The field surrounding a straight current-carrying conductor is shown in Fig. 1.11. The magnetic field defines the direction of motion of a free North pole within the field. In the case of Fig. 1.11, the lines of flux are concentric and the direction of the field determined by the direction of current flow) is given by the right-hand rule.

Magnetic field strength

The strength of a magnetic field is a measure of the density of the flux at any particular point. In the case of Fig. 1.11, the field strength will be proportional to the applied current and inversely proportional to the perpendicular distance from the conductor. Thus:




where B is the magnetic flux density (in Tesla), I is the current (in amperes), d is the distance from the conductor (in metres), and k is a constant.

Assuming that the medium is vacuum or ‘free space’, the density of the magnetic flux will be given by:

The flux density is also equal to the total flux divided by the area of the field. Thus:

In order to increase the strength of the field, a conductor may be shaped into a loop (Fig. 1.12) or coiled to form a solenoid (Fig. 1.13). Note, in the latter case, how the field pattern is exactly the same as that which surrounds a bar magnet. We will see


















 Example

Determine the flux density produced at a distance of 50 mm from a straight wire carrying a current of 20 A.

Example

A flux density of 2.5 mT is developed in free space over an area of 20 cm2. Determine the total flux.
Solution

Ohm’s Law

Local Mobile Advertising
Local Coupons

Provided that temperature does not vary, the ratio of p.d. across the ends of a conductor to the current flowing in the conductor is a constant. This relationship is known as Ohm’s Law and it leads to the relationship:

V / I = a constant = R

where V is the potential difference (or voltage drop) in Volts (V), I is the current in Amperes (A), and R is the resistance in Ohms (see Fig. below).  The formula may be arranged to make V, I or R the subject, as follows:

V = I × R , I = V / R and  R = V / I 

The triangle shown in Fig. A should help you remember these three important relationships. However, it’s worth noting that, when performing calculations of currents, voltages and resistances in practical circuits it is seldom necessary to work with an accuracy of better than ±1% simply because component tolerances are usually greater than this. Furthermore, in calculations involving Ohm’s Law, it can sometimes be convenient to work in units of k< and mA (or M< and µA) in which case potential differences will be expressed directly in V.

 

Example 

A 12 Ohm resistor is connected to a 6V battery. What current will flow in the resistor?

Solution

Here we must use  I = V / R (where V = 6 V and  R = 12 Ohm):

I = V / R = 6 V / 12 Ohm = 0.5 A (or 500 mA)

Hence a current of 500 mA will flow in the resistor.

Example

A current of 100 mA flows in a 56 Ohm resistor. What voltage drop (potential difference) will be developed across the resistor?

Solution

Here we must use  V = I × R and ensure that we work in units of Volts (V), Amperes (A) and Ohms.

V = I × R = 0.1 A × 56 Ohm = 5.6 V

(Note that 100 mA is the same as 0.1 A.) This calculation shows that a p.d. of 5.6 V will be developed across the resistor.

Example

A voltage drop of 15 V appears across a resistor in which a current of 1 mA flows. What is the value of the resistance?

Solution

R = V / I = 15 V / 0.001 A = 15,000 < = 15 kOhm

Note that it is often more convenient to work in units of mA and V which will produce an answer directly in kOhm, i.e.

R = V / I = 15 V/ l mA = 15 kOhm

Basic Real-Time Concepts -- CPU Utilization

Local Mobile Advertising
Local Coupons

CPU Utilization

The final and most important term to be defined is a critical measure of real-time system performance. Because in the von Neumann paradigm, the CPU continues to fetch, decode, and execute instructions as long as power is applied, the CPU will execute either no-ops or instructions or instructions that are not related to the satisfaction of a deadline (for example, noncritical “housekeeping”). The measure of the time spent doing idle processing, in a sense, indicates how much real-time processing is occurring.

Definition: The (CPU) utilization or time-loading factor, U, is a measure of the percentage of non idle processing.

A system is said to be time-overloaded if U> 100%. Systems that are too highly utilized are undesirable because changes or additions cannot be made to the system without risk of time overloading. Systems that are not sufficiently utilized are not necessarily good, because this implies that the system was over engineered and that costs can be reduced with less expensive hardware.

While a utilization of 50% is common for new products, 80% might be acceptable for systems that do not expect growth. However, 70% as a target for U is one of the most celebrated and potentially useful results in the theory of real-time systems where tasks are periodic and independent – a result that will be examined later. Table below gives a summary of certain CPU utilizations and typical situations in which they are associated.

U is calculated by summing the contribution of utilization factors for each (periodic or aperiodic) task. Suppose a system has n ≥ 1 periodic tasks, each with an execution period of pi , and hence, execution frequency, fi = 1/pi .If task i is known to have (or has been estimated to have) a maximum (worst case) execution time of ei , then the utilization factor, ui , for task ei is

ui = ei /pi

Then the overall system utilization is 

 



Note that the deadline for periodic task i, di , is typically the next cycle or time period, and is a critical design factor that is constrained by ei . The determination of the ei either prior to or after the code has been written can be extremely difficult, and in many cases, impossible, in which case estimation must be used. For aperiodic and sporadic tasks ui is calculated by assuming some worst-case execution period, usually the worst-case delay between event occurrences. Such approximations can inflate the utilization factor unnecessarily or can lead to overconfidence because of the tendency to “not worry” about its excessive contribution. The danger is to discover later that a higher frequency of occurrence than budgeted has led to a time-overload and system failure.

The utilization factor differs from CPU throughput, which is a measure of the number of macroinstructions per second that can be processed based on some predetermined instruction mix. This type of measurement is typically used to compare CPU horsepower for a particular application.

Basic Real-Time Concepts -- Events and Determinism

Local Mobile Advertising
Local Coupons

Events and Determinism

In software systems, a change in state results in a change in the flow-of-control of the computer program. Consider the flowchart below.

The decision block represented by the diamond suggests that the stream of program instructions, can take one of two paths, depending on the response in question. if-then, go to, and case statements in any language represent a possible change in flow-of-control. Invocation of procedures in C and Ada represent changes in flow-of-control. In object-oriented languages, instantiation of an object or the invocation of a method causes the change in sequential flow-of-control. In general, consider the following definition.

Definition: Any occurrence that causes the program counter to change non sequentially is considered a change of flow-of-control, and thus an event.

 

In scheduling theory, the “release” time of a “job” is similar to an event.

 

Definition: The release time is the time at which an instance of a scheduled task is ready to run, and is generally associated with an interrupt.

 

Events are slightly different from jobs in that events can be caused by interrupts as well as conditional and unconditional branches.

 

Synchronous and Asynchronous Events

 

An event can be either synchronous or asynchronous. Synchronous events are those that occur at predictable times in the flow-of-control, such as that represented by the decision box in the flowchart  The change in flow-of-control, represented by a conditional branch instruction, or by the occurrence of an internal trap interrupt, can be anticipated (although it may not always occur).

 

Asynchronous events occur at unpredictable points in the flow-of-control and are usually caused by external sources. A clock that pulses “regularly” at 5 milliseconds is not a synchronous event. While it represents a periodic event, even if the clock were able to tick at a perfect 5 milliseconds without drift (which it cannot for physical reasons), the point where the tick occurs with the flow- of-control is subject to many factors. These factors include the time at which the clock starts relative to the program and propagation delays in the computer system itself. An engineer can never count on a clock ticking exactly at the rate specified, and so a clock-driven event must be treated as asynchronous.

 

Events that do not occur at regular intervals (or periods) are called aperiodic. Aperiodic events that tend to occur very infrequently are called sporadic.

 

Table below characterizes a sampling of events.

 For example, an interrupt generated by a periodic external clock represents a periodic but asynchronous event. A periodic but synchronous event is one represented by a sequence of invocation of tasks in a repeated, circular fashion, otherwise known as cyclic code. A typical conditional or unconditional branching instruction that is not part of a code block and that runs repeatedly at a regular rate represents a synchronous but aperiodic event. A branch instruction that happens infrequently, say, on the detection of some exceptional condition, is both sporadic and synchronous. Finally, interrupts that are generated irregularly (randomly) by an external device are classified as either asynchronous aperiodic or sporadic, depending on whether the interrupt is generated frequently or not with respect to the system clock.

 

 Determinism

 

In every system, and particularly in an embedded real time system, maintaining control is extremely important. For any physical system certain states exist under which the system is considered to be out of control; the software controlling such a system must therefore avoid these states. For example, in certain aircraft guidance systems, rapid rotation through a 180◦ pitch angle can cause loss of gyroscopic control. The software must be able to anticipate and avert all such scenarios.

Another characteristic of a software-controlled system is that the CPU continues to fetch and execute instructions from the program area of memory, rather than from data or other unwanted memory regions. The latter scenario can occur in poorly tested systems and is a catastrophe from which there is almost no hope of recovery.

Software control of any real-time system and associated hardware is maintained when the next state of the system, given the current state and a set of inputs, is predictable. In other words, the goal is to anticipate how a system will behave in all possible circumstances.

 

Definition: A system is deterministic if, for each possible state and each set of inputs, a unique set of outputs and next state of the system can be determined.

 

Event determinism means the next states and outputs of a system are known for each set of inputs that trigger events. Thus, a system that is deterministic is event deterministic. Although it would be difficult for a system to be deterministic only for those inputs that trigger events, this is plausible, and so event determinism may not imply determinism.

It is interesting to note that while it is a significant challenge to design systems that are completely event deterministic, and as mentioned it is possible to inadvertently to end up with a system that is nondeterministic, it is also hard to design systems that are deliberately nondeterministic. This situation arises from the difficulties in designing completely random number generators. Deliberately nondeterministic systems would be desirable, for example, as casino gambling machines.

Finally, if in a deterministic system the response time for each set of outputs is known, then, the system also exhibits temporal determinism.
A side benefit of designing deterministic systems is that guarantees can be given that the system will be able to respond at any time, and in the case of temporally deterministic systems, when they will respond. This reinforces the association of control with real-time systems.